2017-11-04

图论应用篇

上次写了篇图的基本构造方法，运用图这种强大的数据结构结构，还能解决实际应用中的许多问题，今天这篇就主要整理一些常见的应用

路径问题

路径问题在图的处理领域是非常重要的。如我们最常见的走迷宫，就是典型的寻路问题。这里主要运用深度优先和广度优先算法两种方式来进行路径寻找，这2种搜索算法在很多数据结构中都有重要的运用，之前写的一篇二叉查找树中的层序遍历就用到了广度优先算法，这里就详细的介绍一下。

1.深度优先寻找路径

首先是深度优先,为了更加形象，直接看下图

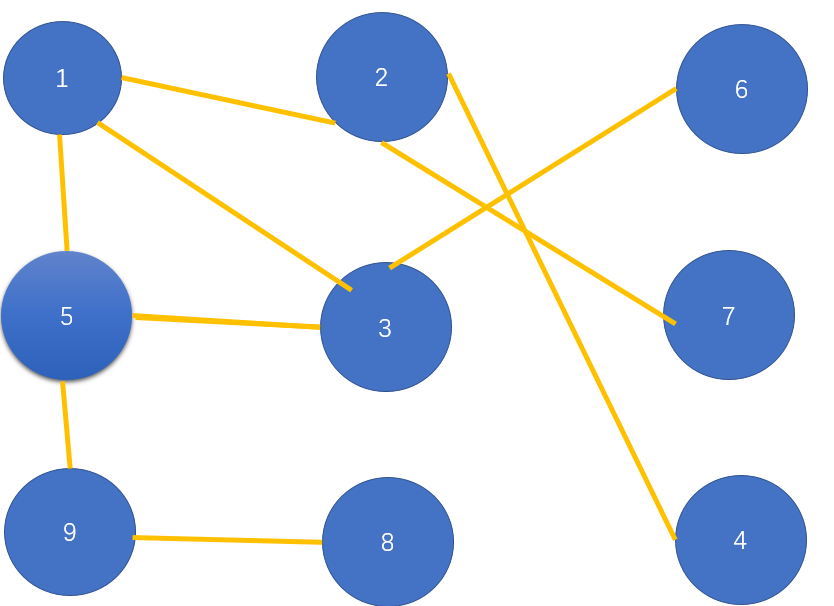
这里以顶点1为出发点，4为终点。假设一个人要走到终点，从1出发有三条路径，首先沿着往5的路径进行遍历，依次1 -> 5 -> 9 -> 8，然后发现没路了，就返回上一顶点，到顶点5这里发现还有一条路就继续沿着这条路走，5->3->6，结果又没路了，就继续返回到起点，沿着另一条路行走……1->2->4，一看，这下就直接到终点了，转了几条路终于找到了终点，那心里真是无比的兴奋啊！回到正题，看看这个具体实现，可以用一个boolean类型的变量来标记是否遍历过该顶点，用一个int型的变量表示从起点到一个顶点的已知路径上的最后一个顶点。至于图的基本构造可以参考我之前写的图论基础篇

/**
 *  图的深度优先查找路径
 * @author Legend
 */
public class DepthFirstPaths {
    private boolean[] marked; // 该顶点是否调用过dfs
    private int[] edgeTo; // 从起点到一个顶点的已知路径上的最后一个顶点
    private final int s; // 起点
    // 图的初始化
    public DepthFirstPaths(Graph G,int s) {
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];
        this.s = s;
        dfs(G,s);
    }
    // 深度优先主方法
    private void dfs(Graph G,int v) {
        marked[v] = true;
        // 遍历与顶点v相连的边
        for (int w : G.adj(v)) {  
            if (!marked[w]) {
                edgeTo[w] = v;
                dfs(G,w);  // 继续递归的进行遍历
            }
        }
    }
   // 是否存在s到v的路径
    public boolean hasPathTo(int v) {
        return marked[v];
    }
   // s到v的路径
    public Iterable<Integer> PathTo(int v) {
        if (!hasPathTo(v)) {
            return null;
        }
        Stack<Integer> path = new Stack<>();
        for (int i = v;i != s;i = edgeTo[i]) {
            path.push(i);
        }
        path.push(s);
        return path;
    }
}

因为我们要准确的知道每一条路径，所以这里创建了一个edgeTo变量用于记录从起点到一个顶点的已知路径上的最后一个顶点，而edgeTo[w] = v表示的就是从w到v的路径。再看PathTo方法，首先判断是否有从s到v的路径，没有就返回null。然后实例化一个Stack类型对象path，依次遍历，把路径上每一个顶点都push进去，最后在push顶点，并返回path。

2.广度优先寻找路径

广度优先正如其名，优先进行广度的遍历，整个过程呈扩散状。这里还是用上面那张图，为了方便查看，还是把图片放到这里。

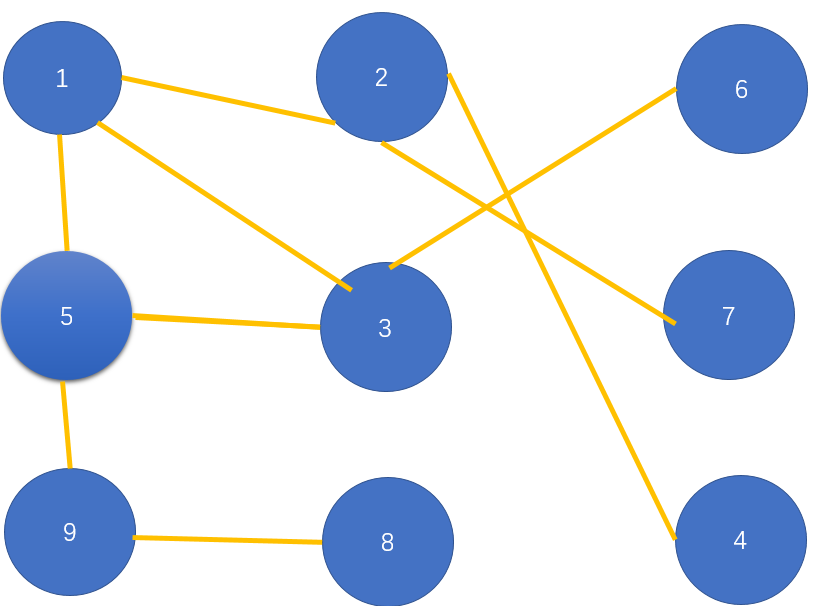
还是用之前的情景，从顶点1出发，先遍历和1相邻的顶点 2,5,3，然后从顶点2开始，右继续遍历和2相邻的顶点，因为已经遍历过顶点1，所以这里就只需要遍历顶点7和顶点4，发然后现就直接到终点了，这是在特殊的情况下，如果先遍历的是另外的顶点，那么几乎要走完每条路才能找到终点。这里就不多说了，重点讲下具体实现，这里用一个抽象数据结构—队列来实现，首先创建一个队列，然后把起点标记后插入队列中去，如果队列不为空就把当前的顶点弹出队列，然后依次遍历和这个顶点相邻的顶点，并把这些顶点标记后也加入队列，接下来用同样的方式将下一顶点弹出队列，遍历和其相邻的顶点，直到队列为空就停止遍历。好了，具体看下面的代码

/**
 *
 * 广度优先寻找路径
 * @author Legend
 **/
public class BreadthFirstPaths {
    private boolean[] marked;
    private int[] edgeTo;
    private final int s;
    public BreadthFirstPaths(Graph G,int s) {
        marked = new boolean[G.V()];
        edgeTo = new int[G.V()];
        this.s = s;
        try {
            bfs(G,s);
        } catch (InterruptedException e) {
            e.printStackTrace();
        }
    }
    private void bfs(Graph G,int s) throws InterruptedException {
        Queue<Integer> queue = new Queue<Integer>();
        marked[s] = true;
        queue.enqueue(s);
        while ( !queue.isEmpty() ) {
            int v = queue.dequeue(); // 从队列中弹出一个顶点
            for (int w : G.adj(v)) { // 遍历和该顶点相邻的顶点
                if ( !marked[w] ) {
                    edgeTo[w] = v; // 保存最短路径的最后一条边
                    marked[w] = true; // 标记它 因为最短路径已知
                    queue.enqueue(w);
                }
            }
        }
    }
    public boolean hasPathTo(int v) {
        return marked[v];
    }
    public Iterable<Integer> pathTo(int v) {
        if ( !hasPathTo(v) ) {
            return null;
        }
        Stack<Integer> path = new Stack<>();
        for (int i = 0;i != s;i =edgeTo[i] ){
            path.push(i);
        }
        path.push(s);
        return path;
    }
}

这里同样运用了pathTo方法，顶点与路径的标记过程和深度优先寻找路径是一样的，这里就不多说了。

连通分量问题

1.介绍

连通分量也是一个比较常见的问题，主要用于判断任意两个结点的连接状态，特别是用于检测网络连接与电路连接的问题中，运用比较广。

2.基本实现

也没什么好说的，这里还是运用深度优先的方法，比较简单，就直接上代码

/**
 * 使用深度优先找出图中的连通分量
 *
 * @author Legend
 * @create 2017-11-01 8:23
 **/
public class CC {
    private int count;
    private boolean marked[];
    private int[] id;
    public CC(Graph G) {
        marked = new boolean[G.V()];
        id = new int[G.V()];
        for (int s = 0;s < G.V();s++) {
            if (!marked[s]) {
                dfs(G,s);
                count++;
            }
        }
    }
    private void dfs(Graph G,int v) {
        marked[v] = true;
        id[v] = count;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                dfs(G,w);
            }
        }
    }
    // 判断两个结点是否相连接
    public boolean isConnected(int v,int w) {
        return id[v] == id[w];
    }
    // v所在连通分量的标识符（0~count-1）
    public int id(int v) {
        return id[v];
    }
    // 连通分量的数量
    public int count() {
        return count;
    }
}

双色问题

1.介绍

能否用2种颜色将图的所有顶点着色，使得任意一条边的两个端点的颜色都不相同,这个问题也就等价于当前的图是不是二分图。因为二叉树其实就是一种比较特殊的图，所以才有这个问题。

2.基本实现

具体实现可以用一个bool类型的变量来表示2种颜色，直接在构造方法里面进行循环，这里也是运用深度优先的方式。首先判断当前结点是否被遍历，没被遍历过就进行遍历，也就是用bool型变量将其标记为true，然后遍历和这个结点相连的结点，并且把这个结点和相邻的结点涂上不同的颜色。然后进行判断
先来看下代码

/**
 * 双色问题
 *
 * @author Legend
 * @create 2017-11-01 9:17
 **/
public class TwoColor {
    private boolean[] marked; //当前结点是否被遍历过
    private boolean[] color; // 表示不同颜色
    private boolean isTwoColorable = true; // 是否能用2种颜色表示
    public TwoColor(Graph G) {
        marked = new boolean[G.V()];
        color = new boolean[G.V()];
        for (int s = 0;s < G.V();s++) {
            if (!marked[s]) {
                dfs(G,s);
            }
        }
    }
    private void dfs(Graph G,int v) {
        marked[v] = true;
        for (int w : G.adj(v)) {
            if (!marked[w]) {
                color[w] = !color[v];
                dfs(G,w);
            } else if (color[w] == color[v]) {
                isTwoColorable = false;
            }
        }
    }
    public boolean isBipartite() {
        return isTwoColorable;
    }
}

如果这2个顶点颜色相同，则不能使得任意一条边的2个端点的颜色都不相同，则这个图不是二分图，试想一下，如果是二分图，任意一条的两个端点肯定颜色是不相同的。因为每次遍历时都将当前顶点与连接顶点标记了2种不同的颜色，如果这个顶点有多个相邻顶点，并且这些相邻顶点又有边相连，这必然会造成2个颜色相同，这样的图自然也不可能是二分图了。

因为这篇博客主要是整理图论的一些应用的问题，所以对于这些问题的优化这里不是重点，有兴趣的可以自己去查查资料，那图论应用篇就暂时到这里了。

赏

纯属好玩